- 受験がすぐそこまで近づいてきて焦ってきた
- 五木模試で良い点をとって中学受験前に自信をつけたい
こんな思いに応えます。
「ばねにはたらく力とかっ車」は特別回以降にしか出ないので、情報が少なく対策しにくいですよね。
過去問でもあれば、事前に勉強できるのにと感じることはないでしょうか?
この記事では「力のはたらきとかっ車」に特化した計算問題を集めています。
思ったような点数が取れず我が子の落ち込む姿に心を痛める前に、過去問で模試対策を行っておきましょう。

応援ねこ
なお、全7回の出やすい問題も解説しています。
一度、目を通しておきましょう。
この記事を読むことで
- 「かっ車」の過去問でつりあいの計算問題が確認できる
- つりあいの式の立て方を知ることで、解法パターンが理解できる
- 中学受験前の五木模試で自信をつけることができる
一問一答形式で「ばねにはたらく力とかっ車」の特訓ができます。

応援ねこ
関連する問題として、「てこのはたらき」も出題されます。
合わせて学習しておきましょう。
五木模試過去問「ばねにはたらく力とかっ車」学習内容
「ばねにはたらく力とかっ車」は、特別回以降で出題されます。
「ばねにはたらく力とかっ車」の学習内容
- ばねにおもりをぶら下げたときのばねの長さを求める計算問題
- 2つのばねをつなげ、2つのばねの伸びの合計からそれぞれの伸びを求める計算問題
- かっ車にぶら下がる棒に加わる力を、棒の端を支点とみなして求める計算問題
- 輪じくの半径の比率をてこの長さの比率と考えてつり合いを考える問題
過去問で勉強し要点をつかみ、模試本番でも解けるようにしておきましょう。
 ポチップ
ポチップ
五木模試過去問「ばねにはたらく力とかっ車」2選
「てこのはたらき」についての過去問を2題集めています。
- ばねにはたらく力と輪じく
- 定かっ車・動かっ車・輪じくのはたらき
ばねにはたらく力と輪じく
平成29年の『第6回』五木模試に出題された「ばねにはたらく力と輪じく」の過去問を解説します。
問題数6問、解答数7問。合計18点。
問題1-1
力のつり合いについて
次の問いに答えなさい。
ばね、棒、かっ車、輪じく、
ひもの重さ、まさつは
考えなくてよい。
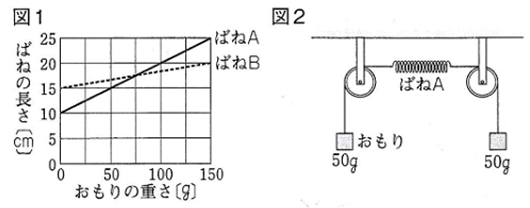
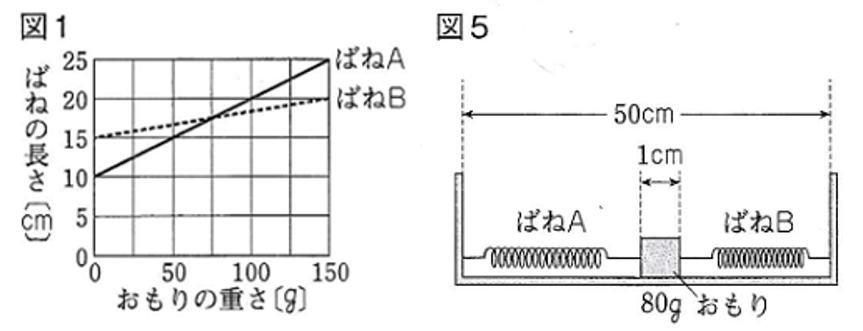
図1は、
2種類のばねA、Bのそれぞれに
おもりをつるしたときの
おもりの重さと
ばねの長さとの関係を
グラフに表したものです。
このばねA、Bを使って
図2~図6のようにしました。
これらはすべてつり合っています。
図2のように、
ばねAの両はしに
50gのおもりをつるした。

ばねAの長さは
何cmになっていますか。
解説を見る
片方の50gのおもりは、かべや天じょうに固定されたのと同じ状態。
つまり、ばねAに50gのおもりを下げたときと同じ。
ばねAに50gのおもりを下げたときのばねAの長さをグラフで読みとると15cm。
ばねを水平にして両側に同じおもりをつり下げつり合っているとき、
片方のおもりはかべで固定された状態と同じ役割をしてるよ

応援ねこ
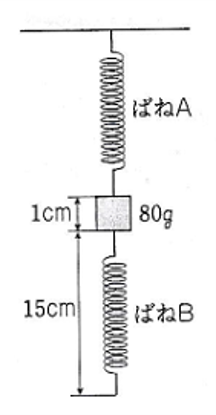
問題1-2
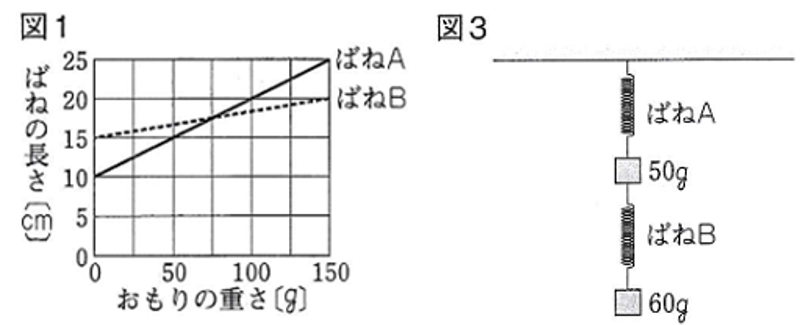
図3のように、
ばねAの下に
50gのおもりをつるし、
その下のばねBに
60gのおもりをつるした。

ばねA、Bの長さは
それぞれ何cmに
なっていますか。
答えをチェック
ばねA:21(cm)
ばねB:17(cm)
(2点×2=4点)
解説を見る
ばねAにかかる力の大きさは、
50 + 60 = 110 (g)
図1より、ばねAは10gで1cmのびるばねなので、 ばねAの伸びは、
110 ÷ 10 = 11 (cm)
ばねAにおもりをつるしてない長さが10cmなので、ばねAの長さは、
10 + 11 = 21(cm)
となる。
ばねBにかかる力の大きさは60g、
図1より、ばねBは30gで1cmのびるので、
ばねBの伸びは、
60 ÷ 30 = 2 (cm)
ばねBにおもりをつるしてない長さが15cmなので、ばねBの長さは、
15 + 2 =17(cm)
となる。
ばねの長さは、
おもりをつるした伸びと元々の長さの合計になるよ

応援ねこ
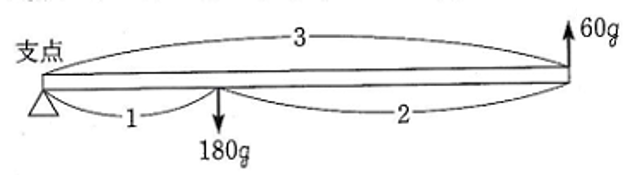
問題1-3
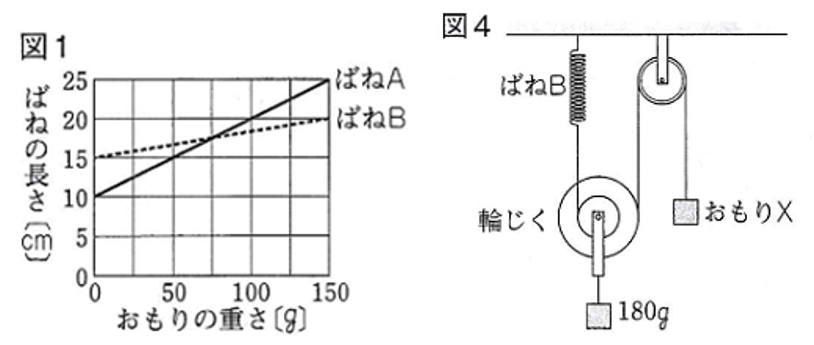
図4のように、
大きい輪と小さい輪の
半径の比が 2:1 である
輪じくの中心に
180gのおもりをつるした。

おもりXの重さは
何gですか。
解説を見る
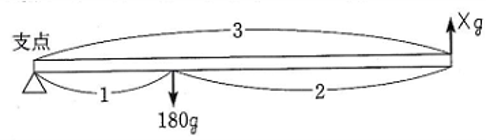
下の図のように、 小さい輪を支えているところを支点として考えると

180 x 1 = X x 3
おもりX = 60 (g)
輪じくを支えているところを支点として、力の向きを作図しよう。
輪じくの輪の半径の比は、てこの長さの比と同じだね。

応援ねこ
解説を見る
ばねBにかかる力は、下の図の支点にかかるカと等しいので
180ー60 = 120 (g)

したがって、ばねBの長さは、
15 + 120 ÷ 30 = 19 (cm)

応援ねこ
問題1-5
図5のように、
重さが80gで1辺が1cmの
立方体であるおもりがある。
ばねA、おもり、ばねBの順で
内側が50cmのわくの中に
固定した。

ばねAの長さは
何cmになっていますか。
解説を見る
ばねAとばねBには80gのおもりの重さはかからない。
つまり、ばねAとばねBには同じ大きさの力がかかっている。
ばねAとBのもとの長さの和は
10 + 15 = 25 (cm)
おもりの幅が1cm、わくの長さが50cmであることから
ばねAとばねBののびの和は、
50ー(25 + 1) = 24 (cm)
となる。
ばねAとばねBの伸びを比較するためにグラフから読み取る。
例えば、150gのおもりのとき、
ばねAは25-15=15cm伸び、
ばねBは20-15=5cm伸びる。
同じ重さのおもりをつるしたときのばねAとBののびの比は3 : 1なので、
Aの伸びは全体の伸びの3/(3+1)倍、
Bの伸びは全体の伸びの1/(3+1)倍となる。
よって、
ばねAの長さ
= 10 + 24 x 3/(3+1)=28(cm)
ばねBの長さ
= 15 + 24 x 1/(3+1)=21(cm)
水平にばねをつなげ、ばねをわくに収めた場合、
2つのばねに同じ力がかかっているよ
全体伸び量が分かれば、伸びの比率から
それぞれのばねの伸びを求めることができます

応援ねこ
問題1-6
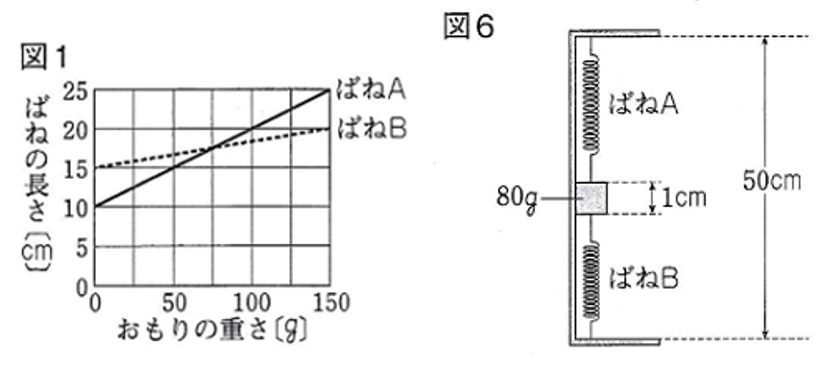
図6のように、
ばねAを上側にして
図5のわくを
まっすぐに立てた。

ばねBの長さは
何cmになっていますか。
解説を見る
図のように、ばねBの下を固定していないときを考える。

ばねAには80gのカがかかるので、ばねAの長さは、
10 + 80 ÷ 10 = 18 (cm)
ばねBのもとの長さは15cmなので、図の全体の長さは、
18 + 1 + 15 = 34 (cm)
図6は、この状態から、ばねBの下に力を加え、あと16cmのばして、全体の長さを50cmにしたもの。
ばねBの下に加えたカと同じ大きさの力がばねAにも加わるので、ばねAとばねBが3 : 1の割合で合計16cmのびている。
したがって、
ばねAの長さ
= 18 + 16 x 3/(3+1)=30(cm)
ばねBの長さ
= 15 + 16 x 1/(3+1)=19(cm)
ばねを垂直につなげ、わくに収めた場合の伸びは、
最初にわくに収めてない状態の伸びから求める。
わくに収めた場合の伸びはわくの幅から求める。
全体の伸び量が分かれば、ばねの伸びの比率から
それぞれのばねの伸びを求めることができる。

応援ねこ
「ばねにはたらく力と輪じく」の過去問を解説しました。
基礎を定着させるために、学んだことを復習しておきましょう。
ばねにはたらく力と輪じく
- ばねを水平にし、両側に同じおもりをつり下げた状態は、片方はかべで固定した状態と同じ
- ばね全体長さは、ばねの元々の長さとおもりをつるした伸びの合計
- 輪じくを支えるひもを支点として、力の向きを作図する
- 輪じくの輪の半径の比は、てこの長さの比と同じ
- 輪じくを支えている支点にかかる力と同じ力が上向きにかかる
- 2つのばねを水平につなげ、ばねをわくに収めた場合、2つのばねにかかる力は同じ
- 2つのばねのそれぞれの伸びは、全体の伸び量と2つのばねの伸びの比率から求める
- 2つのばねを垂直につなげ、わくに収めたときの伸びは、わくに収めてない状態の長さと、わくの長さの差が2つのばねの伸びの合計
- 全体の伸び量が分かれば、ばねの伸びの比率からそれぞれのばねの伸びを求められる
定かっ車・動かっ車・輪じくのはたらき
平成29年の『第6回』五木模試に出題された「定かっ車・動かっ車・輪じくのはたらき」の過去問を解説します。
問題数2問、解答数2問。合計8点。
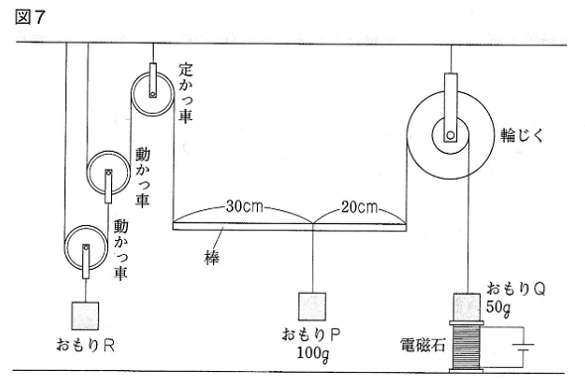
問題2-1
100gのおもりP
鉄でできた50gのおもりQ
重さのわからないおもりR
長さが50cmの棒、
輪じく、かっ車、電磁石を使い
図7のような装置をつくった。
輪じくは
大きい輪と小さい輪の
半径の比が 2:1 です。
このとき、
棒は水平につり合っていて、
装置はすべて静止しています。

おもりRの重さは
何gですか。
解説を見る
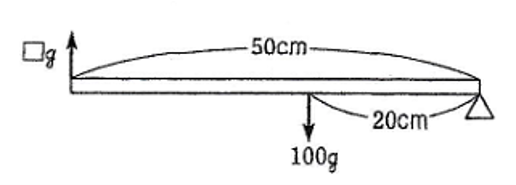
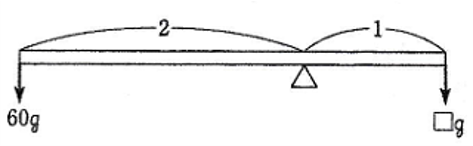
次の図のように、棒の右はしを支点とし、棒の左はしにかかる力を□gとして考えると、
□×50=100×20
□ =40(g)

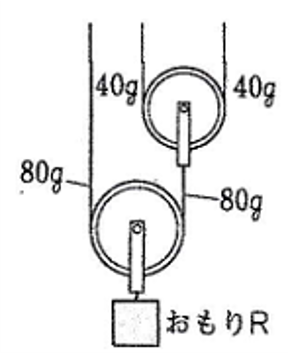
下の図のように、上の動かっ車のひもにかかる力が40gなので、下の動かっ車のひもにかかる力は、
40×2=80(g)

したがって、
おもりRの重さ= 80×2=160(g)
かっ車にぶら下がった棒の端を支点として力のつり合いを考えよう
力の大きさを求めたい方とは逆の端を支点とするのがポイントだよ

応援ねこ
問題2-2
電磁石が
鉄でできたおもりQを
引いている力は、
重さが何gのおもりを
おもりQにつるしたときと
同じですか。
解説を見る
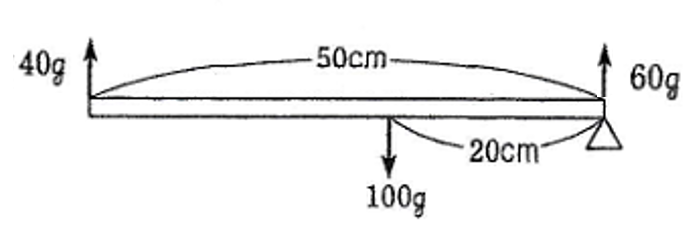
棒の右はしにかかる力は図のように
100-40=60(g)

輪じくの中心を支点として、てこの力を考えると、下の図になる。
小さい輪にかかっているひもにかかる力を□gとすると、
60×2=□×1
□=120 (g)

したがって、電磁石がおもりQを引いている力の大きさは、
120-50=70(g)
棒の支点に加わる力は、棒にかかる力の向きのつり合いから求める
輪軸の半径の比は、てこの長さの比と同じ

応援ねこ
「定かっ車・動かっ車・輪じくのはたらき」の過去問を解説しました。
学んだことのまとめになります。
定かっ車・動かっ車・輪じくのはたらき
- かっ車にぶら下がった棒の端を支点として、力のつり合いを考える
- 力の大きさを求めたい方とは逆の端を支点とする
- 棒の支点に加わる力は、棒にかかる力の向きのつり合いから求める
- 輪軸の半径の比は、てこの長さの比と同じ
「ばねにはたらく力とかっ車」まとめ
今回は五木模試で出題された「ばねにはたらく力とかっ車」の過去問を紹介しました。
- ばねにはたらく力と輪じく
- 定かっ車・動かっ車・輪じくのはたらき
解法パターンを理解し苦手な計算を克服しておきましょう。
 ポチップ
ポチップ