- 特別回から「てこのはたらき」が出るってホント?
- 受験が近づいてきてるし、五木模試の結果が悪いと落ち込みそう
こんな悩みはないでしょうか?
過去問で勉強できれば前もって準備できるのにと、思っているのではないでしょうか。
特別回は受験校で模試が受験できるので、良い点を取って自信をつけたいですよね。
この記事では、計算問題の多い「てこのはたらき」を紹介しています。
やり方さえ分かればどれも同じ問題だと理解できると思います。
五木模試が終盤になると、嫌でも中学受験を意識せざるを得ないと思います。
中学受験前の五木模試で自信をつけ、お子様の笑顔が増えることを願っております。

応援ねこ
なお、全7回の出やすい問題も解説しています。
過去の出題傾向も目を通しておきましょう。
この記事を読むことで
- 「てのはたらき」の過去問で計算問題の練習ができる
- 志望校で受験できる特別回で自信をつけることができる
どこが重要かを分かった上で勉強を進められるので、効率良く基礎固めができます。

応援ねこ
関連する問題として、「ばねにはたらく力とかっ車」も良く出題されます。
こちらの過去問も合わせて学習し、学びを深めておきましょう。
五木模試過去問「てこのはたらき」学習内容
「てこのはたらき」は、特別回から出題され、次の内容を学習します。
「てこのはたらき」の学習内容
- さおばかりの皿に乗せた物体の重さを、おもりの移動距離から求める
- 針金を用いた平面のつり合いは、行・列それぞれに対してつり合いの式を立てることで解決する
- 力の大きさと力の向きを作図し、つり合いを考えることで台ばかりに加わる重さを求める
- 太さの異なる棒の断面積と長さから重心を求め、つり合いの式を立てる
実験形式の「てこのはたらき」について出題されます。
過去問で要点をつかみ、模試本番でも計算できるようにしておきましょう。
 ポチップ
ポチップ
五木模試過去問「てこのはたらき」4選
「てこのはたらき」についての過去問を4題集めています。
- さおばかり
- 針金を用いた平面上のつり合い
- 台ばかりの指すおもさ
- 太さが一様でない棒の重心
さおばかり
2021年の『特別回』五木模試に出題された「さおばかり」に関する過去問を解説します。
問題数5問、解答数5問。合計10点。
問題1-1
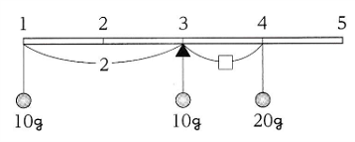
太さが一様で長さが100cm
重さが100gの棒と
重さが200gの皿
100gのおもりを使って
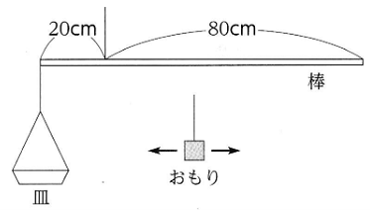
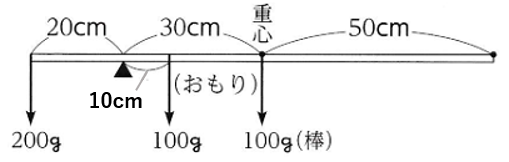
図のようなさおばかりをつくった。
左はしから
20cmのところをひもでつるし
左はしに皿をつるした。
ただし、
おもりは棒の
左はしから右はしまで
どこにでもつるせるものとし、
ひもの重さは考えないものとする。

0gを示す目盛りは
左はしから何cmのところに
つけられていますか。
解説を見る
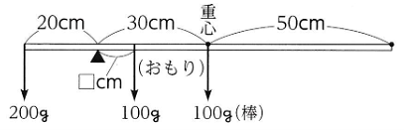
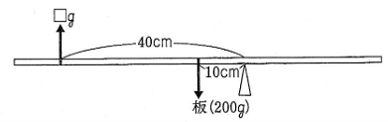
棒の重さは棒の中心(重心)にすべてかかる。
下の図のようなつりあいになり
支点(ひもをつるした点)からの距離を口cmとすると

200×20=100×30+100×□
□=10(cm)
よって、左はしからは、
20+10=30(cm)
ひもをつるした点を支点として、
棒にかかっている力を矢印で書く
皿におもりが乗ってない状態のつり合いの式を立てる

応援ねこ
問題1-2
10gを示す目盛りは
左はしから何cmのところに
つけられていますか。
解説を見る
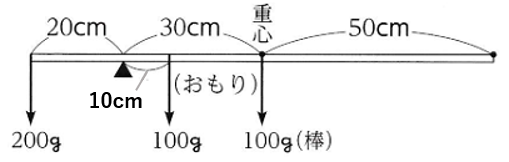
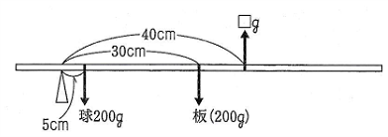
前問から、さおばかりが0gのときのつり合いは下の図になる。

皿の上に10gの物体をのせたときにふえる反時計まわりのモーメント(回そうとするカ)と
100gのおもりを右に移動したときにふえる時計まわりのモーメントがつりあえばよい。
0gの目盛りから移動する長さを□cmとすると
10×20=100×□
□=2(cm)
よって、左はしからは、
30+2=32(cm)
皿におもりを乗せてない状態を基準にする
皿に物体を乗せたときのおもりの移動距離を考えよう

応援ねこ
問題1-3
皿に80gの物体をのせたとき、
おもりを左はしから
何cmのところにつるせば
つりあいますか。
解説を見る
前問から、皿に10gの物体を乗せたとき、つり合いを保つためには100gのおもりを右に2cm移動させる必要がある。
皿に80gの物体を乗せた場合は、左はしから、
30+2×(80÷10)=46(cm)
皿に物体を乗せたとき、おもりは何cm移動させる必要があるかを考える
物体の重さとおもりの移動距離の関係から問題を解けるようにしよう

応援ねこ
問題1-4
皿にある重さの物体をのせたとき
おもりを左はしから
86cmのところにつるすと
つりあいました。
皿にのせた物体の重さは
何gですか。
解説を見る
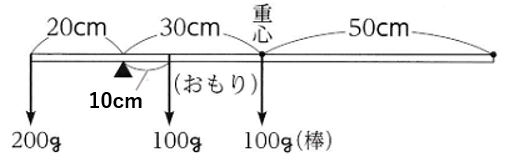
下の図は皿に物体が乗ってないときの図。

皿に10gの物体を乗せたとき、つり合いを保つためには100gのおもりを右に2cm移動させる必要がある。
おもりを左はしから86cmのところにつるすので、100gのおもりを右に移動させた距離は
86-30=56(cm)
皿に10gの物体を乗せるとき、100gのおもりを右に2cm移動させるので
(56÷2)×10=280(g)
おもりを移動させた距離が分かれば、
皿に何gの物体を乗せたかが分かるね

応援ねこ
問題1-5
このさおばかりは、
何gの重さまで
はかることができますか。
解説を見る
図は0gの目盛りの場合(皿に物体が乗ってない場合)の図。

この状態から100gのおもりを最大70cm右へ移動できる。
皿に10gの物体を乗せるとき、100gのおもりを右に2cm移動させるので
このさおばかりがはかることのできる重さは
(70÷2)×10=350(g)
さおの端までおもりを移動させた状態が
さおばかりではかれる最大重さ

応援ねこ
「さおばかり」の五木模試過去問を解説しました。
学んだことのまとめになります。
さおばかり
- ひもをつるした点を支点として、棒にかかっている力を矢印で書き、皿に物体が乗ってない状態のつり合いの式を立てる
- 皿に物体を乗せてない状態を基準として、皿におもりを乗せたときのおもりの移動距離を考える
- 皿に物体を乗せたとき、おもりをどれだけ移動させるかを考えるためにつり合いの式を立てる
- さおばかりは、皿に乗せた物体の重さに対するおもりの移動距離の関係を知ることが大切
- さおの端までおもりを移動させた状態が、さおばかりではかることのできる最大の重さ
さおばかりは、こちらの実験キットで学ぶこともできます。
 ポチップ
ポチップ
針金を用いた平面上のつり合い
2021年の『第6回』五木模試に出題された「針金を用いた平面上のつり合い」の過去問を解説します。
問題数3問、解答数3問。合計6点。
問題2-1
針金を使って
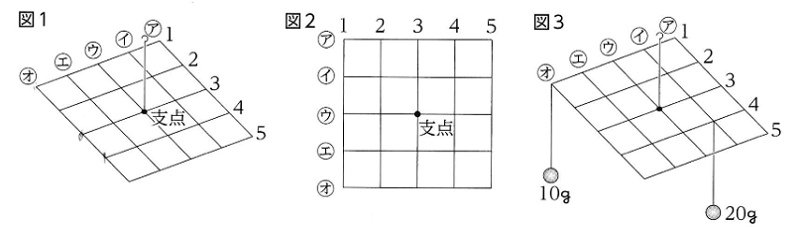
図1のような装置をつくり
その中心をひもでつるすと
水平につりあいました。
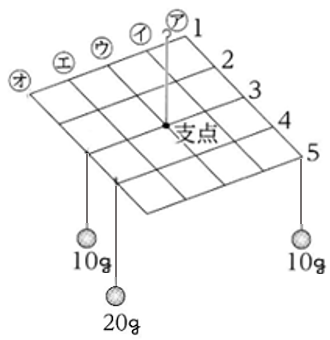
図2は
この装置を真上から見たもので
各わくは同じ大きさの
正方形になっています。
また、 針金の交わる点や角には
おもりをつるせるようになっていて
図3のようにおもりをつるした場合
10gのおもりをつるした位置は
( オ、1 )
20gのおもりをつるした位置は
( イ、4 )と表し
図3の装置は水平に
つりあっているものとします。

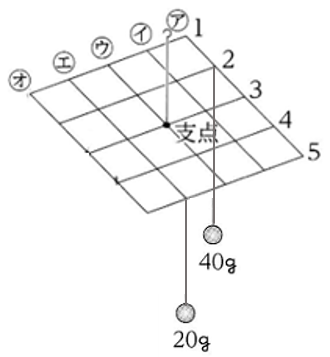
図1の装置の
(ア、3 )と(オ、1 )のそれぞれに
10gのおもりを1個ずつ
つるしました。

20gのおもりを1個つるして
水平につりあわせるためには
どこにつるせばよいですか。
(ア、1)のように答えなさい。
解説を見る
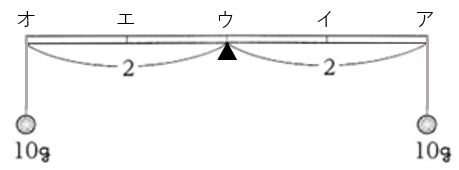
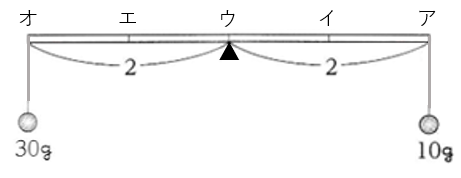
ア~オ(これを行とする)を横にして考えると、 下の図のように、2つの10gのおもりから支点までのきょりがそれぞれ等しくなります。下の図において、20gのおもりは支点と同じウの行につるすとつり合います。

次に、1~5 (これを列とする)を横にして考えると、下の図のように(ウ、3)の10gのおもりは支点の位置になります。
そして、支点から20gのおもりまでのきょりを□として、(オ、1)にある10gのおもりとつり合いを考えると、

10×2=20×□
□=1(目盛り)となるため、
20gのおもりは支点から右へ1目盛りはなれた4の列となります。
したがって、 20gのおもりをつるす位置は( ウ 、 4 )となります。
行と列のそれぞれの向きに対して、つり合いを考えよう

応援ねこ
問題2-2
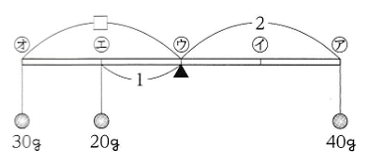
図1の装置の
(ア、2 )に40gのおもりを1個
(エ、5 )に20gのおもりを1個
つるしました。

30gのおもりを1個つるして
水平につりあわせるためには
どこにつるせばよいですか。
(ア、1 )のように答えなさい。
解説を見る
ア~オを横にして考え、次の図のように支点から30gのおもりまでのきよりを□とすると、
30×□+20×1=40×2
□=2(目盛り)
となるため、30gのおもりは支点から左へ2目盛りはなれたオの行となります。

1~5を横にして考えると、 40×1 = 20×2と30gのおもりをつるさなくてもつりあっているので、 30gのおもりをつるす位置は支点と同じ3の列となります。したがって、 30gのおもりをつるす位置は ( オ、3 )となります。

行と列のそれぞれの向きに対して、つり合いを考えよう

応援ねこ
問題2-3
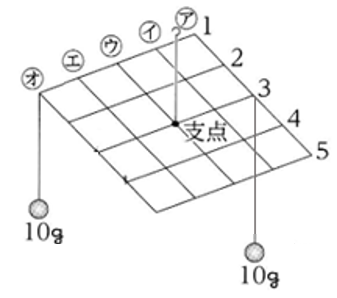
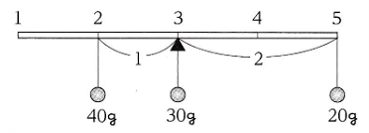
図1の装置の
(ア、5 )と(オ、3 )に
10gのおもりを1個ずつ、
(オ、4)に20gのおもりを1 個
つるしました。

20gのおもりを1個つるして
水平につりあわせるためには
どこにつるせばよいですか。
(ア、1)のように答えなさい。
解説を見る
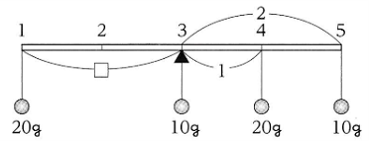
ア~オを横にして考えると、下の図のように支点から左に2目盛りの位置に30g、右に2目盛りの位置に10gかかっている状態となります。

20gのおもりを右に2目盛りのアの行につるすことでつり合います。
1~5を横にして考え、支点から最後に左に加える20gのおもりまでのきょりを□とすると、下の図のように表すことができます。

つりあいの式を立てると
20×□=20×1+10×2
□=2(目盛り)
となります。
20gのおもりは支点から左へ2目盛りはなれた1の列となります。
したがって、 20gのおもりをつるす位置は( ア、 1 )となります。
行と列のそれぞれの向きに対して
つり合いを考えることで、
すべての問題が解けることが分かったね

応援ねこ
「針金を用いた平面上のつり合い」の五木模試過去問を解説しました。
基礎を定着させるために、学んだことを復習しておきましょう。
針金を用いた平面上のつり合い
- 平面上のつり合いは、行と列のそれぞれの方向から見たつり合いを考える
台ばかりの指すおもさ
平成30年の『第6回』五木模試に出題された「台ばかりの指すおもさ」に関する過去問を解説します。
問題数5問、解答数6問。合計18点。
問題3-1
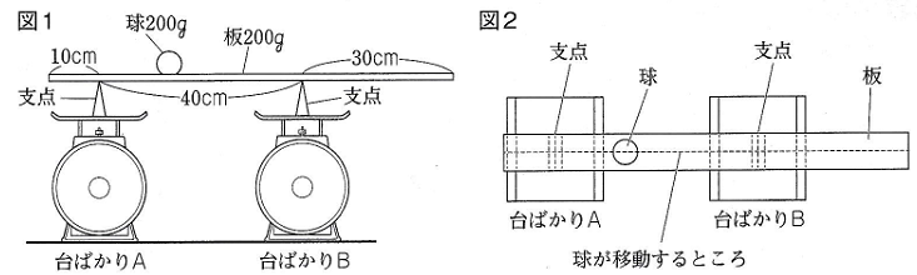
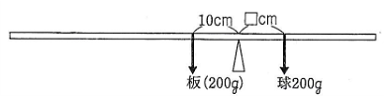
図1のように、
長さ80cm、重さ200gで
厚さやはばが均一な板がある。
台ばかりA、Bの上にのせた
三角柱の支点の上に板をのせ、
その板の上に
重さ200gの球を置いた
(図2は真上から見たようす)。
ただし、
球はつねに板の中心を通る線
(図2の一一)に置くものとします。
また、支点の重さは
考えないものとします。

球を置く前、
台ばかりAは
何gを示していましたか。
解説を見る
台ばかりAの上の支点に加わる力を□gとして、台ばかりBの上の支点をてこの支点とすると、球が乗ってない状態のつり合いは下の図のようになるので、

□×40 = 200×10
□ = 50 (g)
台はかりに乗っている支点は
上向きの力で板を支えているよ

応援ねこ
問題3-2
球を板の左はしから
15cmのところに置きました。
台ばかりBは
何gを示していましたか。
解説を見る
台ばかりAの支点から右に5cmのところに200gの球があります。
また、台ばかりAの支点から30cmのところに200gの板の重心があります。
台ばかりBの上の支点に加わる力を□gとして、 台ばかりAの上の支点をてこの支点とすると、次の図のようなつり合いとなるので、

200×5 + 200×30 = □×40
□ = 175(g)
支点からの距離と力の向きを作図し、
つり合いの式を立てよう

応援ねこ
問題3-3
球を板のある位置に置いたとき
台ばかりAが100gを示した。
球を置いた位置は
板の右はしから
何cmのところですか。
解説を見る
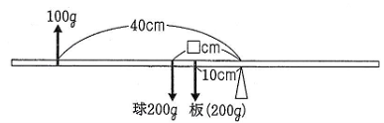
台ばかりAの示す値が50gより大きく250gより小さいので、球は台ばかりAの上の支点と台ばかりBの上の支点の間にあることがわかります。よって、台ばかりBの上の支点をてこの支点として、ここから球までの長さを□cmとすると、下の図のようなつり合いとなるので

100×40 = 200×□ + 200×10
□ = 10(cm)
(たまたま、板の重心と同じ位置になった)
よって、板の右はしからの長さは、
30+10 = 40(cm)

応援ねこ
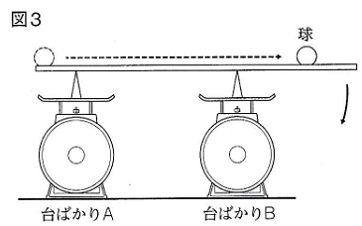
問題3-4
図3のように、
球を板の左はしから右はしへ
ゆっくりと移動させると
球がある位置を通過したときに
板が右にかたむきはじめた。

板が右にかたむきはじめるのは
球が板の左はしから
何cm移動したときですか。
解説を見る
板が右にかたむきはじめるとき、台ばかりAの上向きの力はゼロになります。
台ばかりBの上の支点をてこの支点として、ここから球までの長さを□cmとすると、下の図のようなつり合いとなるので、

200×□ = 200×10
□ = 10(cm)
したがって、板が右にかたむきはじめるときの板の左はしから球までの長さは、
10+40+10 = 60(cm)
台ばかりから板が離れるとき、
台ばかりにかかる力はゼロになるよ

応援ねこ
解説を見る
板が台ばかりAから離れるので、台ばかりに加わる力はなく、0gとなります。
板と球の重さはすべて台ばかりBの上の支点に加わるので、台ばかりBに加わる力は、
200+200 = 400(g)
支点が一つのときは、
すべて重さは一つの支点に集中するよ

応援ねこ
「台ばかりの指すおもさ」の五木模試過去問を解説しました。
学んだことを復習しておきましょう。
台ばかりの指すおもさ
- 支点からの距離と力の向きを作図し、つり合いの式を立てる
- 台ばかりの指す力は上向きで作図する
- 台ばかりから板が離れるとき、台ばかりにかかる力はゼロになる
- 支点が一つのとき、すべて重さは一つの支点に集中する
太さが一様でない棒の重心
平成29年の『第6回』五木模試に出題された「太さが一様でない棒の重心」に関する過去問を解説します。
問題数2問、解答数2問。合計4点。
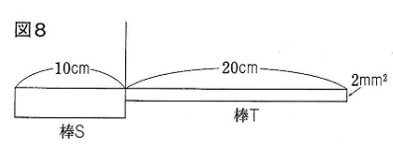
問題4-1
図のように、
長さが10cmで断面積がわからない棒Sと
同じ材質でできた
長さが20cmで断面積が2mm2である棒Tを装着し、
そのつなぎ目をひもでつるしたところ、
棒は水平につり合った。

棒Sと棒Tでは、どちらのほうが重いですか。
ア 棒Sのほうが重い
イ 棒Tのほうが重い
ウ 同じ重さである
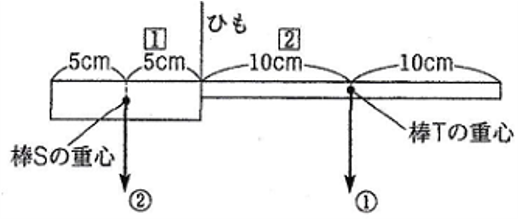
解説を見る
下の図のように、
ひもから棒Sの重心までの長さは5cn、
ひもから棒Tの重心までの長さは10cm

棒Sの重さ:棒Tの重さ
=10:5
=2:1
となります

応援ねこ
解説を見る
同じ材質でできているので、
重さは体積に比例します。
よって、
棒Sの体積は棒Tの体積の2倍です。
棒Sの断面積は
20(cm)×2(mm2)×2÷10(cm)
=8(mm2)
太さが一様でない棒の重心
- 同じ材質の棒のつり合いは、「棒の長さ×断面積×棒の中心」から棒の重心に加わる力のつり合いを考える
五木模試過去問「てこのはたらき」まとめ
今回は五木模試で出題された「てこのはたらき」を過去問で学習しました。
- さおばかり
- 針金を用いた平面上のつり合い
- 台ばかりの指すおもさ
- 太さが一様でない棒の重心
記憶に定着させるため、解けなかった問題を復習しておきましょう。
 ポチップ
ポチップ